IL CALENDARIO PERPETUO
"Gli anni che fuggono inarrestabilmente ci portano via una cosa dopo l'altra"
Quinto Orazio Flacco (65 a.C. - 8 a.C.)
Il calendario perpetuo permette di determinare il giorno della settimana (lunedì, martedì, mercoledì, giovedì, venerdì, sabato e domenica) di una qualsiasi data del calendario.
Basandosi su un reiterato algoritmo, la ricerca può essere estesa a centinaia e addirittura a migliaia di anni.
Uno degli algoritmi più noti è quello creato da F. Berio consistente nel sommare 5 termini, facendo uso dell'operazione di modulo per ridurre il risultato della somma ad un valore inferiore a 7. Tale operazione (indicata dal simbolo "mod") è analoga all'aritmetica dell'orologio (secondo cui ad es. le ore 15 corrispondono alle ore 3 poiché 15 mod 12 = 3) e consiste nel resto della divisione (quindi 18 mod 7 = 4 poiché 18 / 7 = 2 e il resto della divisione è 4; o, equivalentemente, poiché togliendo 7 due volte da 18, il resto vale 4).
L'aritmetica modulare (anche detta "aritmetica dell'orologio" poiché su questo principio si basa il calcolo delle ore a cicli di 12 o 24) rappresenta un importante ramo della matematica. Trova applicazioni nella crittografia, nella teoria dei numeri (in particolare nella ricerca dei numeri primi) ed è alla base di molte delle più comuni operazioni aritmetiche e algebriche, nonchè il principio su cui si basa il calendario perpetuo.
Si tratta di un sistema di aritmetica degli interi, in cui i numeri "si avvolgono su loro stessi" ogni volta che raggiungono i multipli di un determinato numero n, detto modulo. L'aritmetica modulare e la notazione usuale delle congruenze vennero formalmente introdotte da Carl Friedrich Gauss nel suo trattato Disquisitiones Arithmeticae, pubblicato nel 1801.
La relazione di congruenza
L'aritmetica modulare si basa sul concetto di congruenza modulo n. Dati tre numeri interi a, b, n, con n ≠ 0, diciamo che a e b sono congruenti modulo n, oppure che a è congruo a b modulo n, se la differenza (a − b) è un multiplo di n. In questo caso scriviamo:
Per esempio possiamo scrivere:
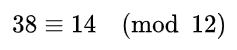
poiché 38 − 14 = 24, che è un multiplo di 12.
Nel caso entrambi i numeri siano positivi, si può anche dire che a e b sono congruenti modulo n se hanno lo stesso resto nella divisione per n. Quindi possiamo anche dire che 38 è congruo a 14 modulo 12 poiché sia 38 sia 14 hanno resto 2 nella divisione per 12.
Il seguente file Microsoft Office Excel offre un calendario perpetuo dall'anno 1 all'anno 5.000 (tappa sull'icona per avviare il download):
Il calendario perpetuo è stato realizzato con l'ultima versione di Excel disponibile, ovvero la versione 2019 di Microsoft Office. E' quindi garantita la retrocompatibilità fino alla versione 2007 del software.
Seguite le istruzioni contenute nel file per scoprire ad esempio in che giorno della settimana siete nati.
Buona ricerca a tutti!
HAI GIA' RICEVUTO LA TUA PASSWORD MF?
Clicca sul pulsante verde e utilizzala insieme alla tua e-mail per accedere all'area riservata.





